To understand how this equation works, we first need a crash course (or a friendly refresher) in boundary layer meteorology. The boundary layer is a well mixed layer that develops near the surface throughout the day due to the heating from the sun. In a strict definition, the boundary layer is the layer of air that is in communication with the earth’s surface through the process of turbulent transfer. Early in the morning when the sun rises, the amount of solar radiation that reaches the earth’s surface is small. However, as the sun rises, the amount of solar radiation reaching the surface increases. As the amount of energy intensifies, the surface of the earth heats the air from below. The more intense solar energy this is, the faster the boundary layer grows. The boundary layer increases in height throughout the day through turbulence and mixing. Turbulent eddies distribute both heat and moisture throughout the boundary layer. The depth of the boundary layer is dependant on many quantities including cloud cover, stability of the atmosphere and time of year. The depth of the boundary layer can vary from a few hundred meters (~700 ft) to several kilometers depending on these varying quantities.
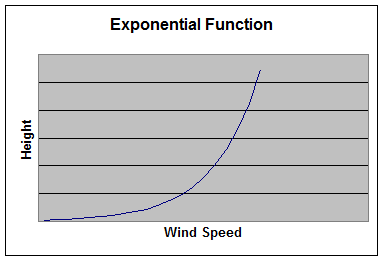
Because of turbulent eddies driven by solar heating that are constantly redistributing the air, certain properties of the atmosphere are constant throughout the mixed layer. Other properties, such as the winds speed are not constant through the mixed layer, but have been studied and are well understood. The measured wind speed is dependant on the roughness of the surface in the area around the observations. As the surface becomes increasingly rough, we would expect winds to be less in the lower part of the boundary layer due to friction. With an increase in height, the wind speed increases similar to that shown in figure 1. Through research, it was found that the shape of the wind profile in the boundary layer is similar to the graph of an exponential function. Therefore, if we can arrive at an estimate of the surface roughness, we can estimate the wind speed in a well mixed boundary layer.
This method is good for determining the wind speeds aloft in the afternoon and evening hours after a well mixed layer has developed. Because mixing does not take place overnight, this method would not be able to capture various features such as the low level jet and thus would not be useful for estimating wind speeds for morning flights.
In the next issue, I will present the equation that can be used to find the wind speed at any altitude in the mixed layer along with a few examples.
Fig.1 Wind speed increases with height as an exponential function.
In the last issue, we saw that the wind speed with respect to height in a well mixed boundary layer can be approximated using an exponential function. In this article, we will explore an equation that can be used to find the wind speed at any height in the boundary layer (mixed layer).
The formula itself is fairly simple and straight forward:
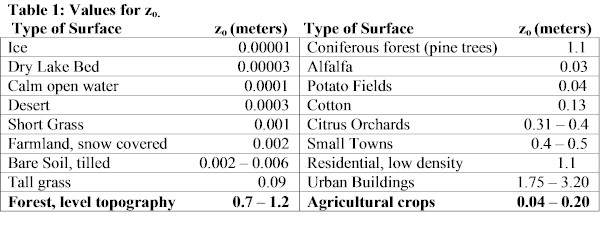
where u* is called the friction velocity, z is the height (in meters) of the observation or level you would like to compute the wind at, zo is called the roughness parameter that is based on the surface characteristics(table 1) and U(z) is the wind speed in meters per second. The friction velocity is constant throughout the entire boundary layer. The natural log function in this equation comes from the fact that the wind speed is exponential with height. The inverse of an exponential function is a logarithmic function. We need to use the logarithmic function because we are solving for the wind speed and not for the height.
Let’s apply this formula to a few examples:
On a warm sunny July day, the 5 PM news reports a wind speed at O’Hare International Airport of 9 mph (4 meters per second). What is the wind at 300 meters (~1000 ft) in the atmosphere assuming the boundary layer extends higher than this?
It is important to note that most surface wind measurements are taken at 10 meters. First, we need to estimate the type of surface found at and around the observation. O’Hare is surrounded by a very urban setting since it lies in the middle of downtown Chicago. Because it is such an urban setting, you might think we should use a value near the upper threshold for an urban setting. However, the observing equipment is located out in the middle of the tarmac, and is therefore more exposed than equipment would be located next to the base of the Sears Tower. To account for this, we will use a roughness parameter of 2.7(see table 1). Now, we need to use the wind speed to determine the friction velocity.
Using the equation from above we get:
where the 4 on the left hand side of the equation is our wind speed in meters per second, the 10 in the natural log term comes from the observation height (10 meters) and 2.7 is from the assumptions we made about the surface near the airport. Therefore we need to rearrange this formula so we can solve for u*.
First we move the 0.4 to the other side of the equation:
Then, we need to move the natural logarithm on the right hand side of the equation to the left hand side. If we divide each side of the equation by ,
then we get the following:
Plugging this into a calculator, you get u* = 1.222 meters per second.
Since this value is constant throughout the boundary layer, we can use the information we have to solve for the wind at any height. Therefore, if we wanted to find the wind speed at 300 meters, we get:
where u* = 1.222 meters per second, z = 300 (the height of the wind speed in meters that we are interested in) and zo= 3.1. Therefore we get,
, which equals 14.391 meters per second or about 32.19 miles per hour. Not exactly ideal ballooning conditions!
Let’s suppose instead that the wind speed was recorded by a school net station. The height above ground level at which the school net station makes measurements varies because most (if not all) the school net weather stations are on the roof of the school. To keep things simple, I will assume the height of the school to be 10 meters. For this case, we will also assume a hot, sunny day in July. Therefore, the only thing changing in this problem will be the surface roughness parameter due to the terrain around the school. Most schools are located in the town or city, so we would expect the surface roughness parameter to be higher than it would be in open country. To arrive at an estimate of the surface roughness parameter, let assign a specific school to this problem. Since Indianola, Iowa is a popular place to fly, let choose the school there. The only schoolnet station in Indianola is located at Emerson Elementary School. Emerson Elementary School is located in a sparsely populated residential area. Therefore, we could assume a roughness parameter of around 1.1. Assuming this roughness parameter, we can calculate the wind speed at any height in the boundary layer. In this case, as in the last, we will assume a wind speed of 9 mph was measured.
Plugging these values into our equation for the various values, we get:
Solving for u*, we get
meters per second
Solving for the wind at 300 meters (~1,000 ft), we get
meters per second which is approximately 22.73 mph.
These examples show how important it is to arrive at an accurate estimate of the surface roughness parameter. The surface roughness parameter can change both due to location and season. This also shows how dependant the strength of the wind is based on the surface below. Once you arrive at an estimate of the surface characteristics, using this simple equation will give you an estimate of the wind speed at any height in the mixed layer near the surface.



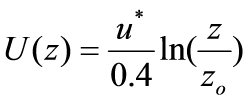

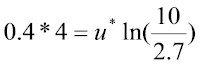
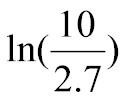
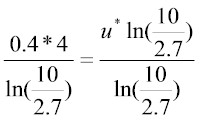
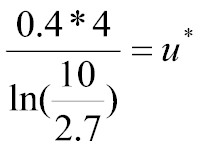
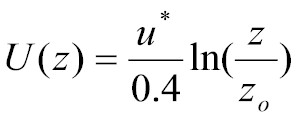
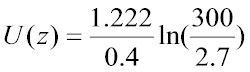
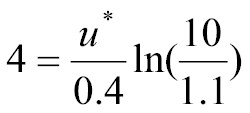
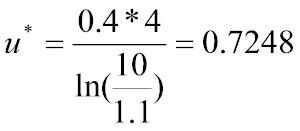
















.jpg.63107fd0779ec1d149efb68987df502e.jpg)














Recommended Comments
There are no comments to display.
Join the conversation
You are posting as a guest. If you have an account, sign in now to post with your account.
Note: Your post will require moderator approval before it will be visible.